合并区间、不同路径、岛屿的最大面积

合并区间

题目描述

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi]。请合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]

输出：[[1,6],[8,10],[15,18]]

解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6]

思路

一个区间可以表示为 [start, end]，先按区间的 start 排序：

对于几个相交区间合并后的结果区间 x，x.end 一定是这些相交区间中 end 最大的

注意：

在解题时可以直接先把 intervals[0] 推入 res，后续通过比较 res 的最后一个元素和 intervals[i] 来决定新增区间（last[1] < start）还是改变 end 大小（last[1] = Math.max(end, last[1])），防止漏掉最后一个区间

题解

tsCopy
function merge(intervals: number[][]): number[][] {
  intervals = intervals.sort((a, b) => a[0] - b[0]);
  let res = [];

  res.push(intervals[0]);

  for (let i = 1; i < intervals.length; i++) {
    const last = res[res.length - 1];
    const [start, end] = intervals[i];

    if (start > last[1]) {
      res.push(intervals[i]);
      continue;
    }

    last[1] = Math.max(end, last[1]);
  }

  return res;
}

不同路径

题目描述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例：

输入：m = 3, n = 7

输出：28

思路

状态转移方程：dp[i][j] = d[i - 1][j] + dp[i][j - 1];

base case: dp[0][0] = 1;

题解

tsCopy
function uniquePaths(m: number, n: number): number {
  const memo = Array.from({ length: m }, () => new Array(n));

  const dp = (i, j) => {
    if (i === 0 && j === 0) {
      return 1;
    }

    if (i < 0 || j < 0) {
      return 0;
    }

    if (memo[i][j]) {
      return memo[i][j];
    }

    memo[i][j] = dp(i - 1, j) + dp(i, j - 1);
    return memo[i][j];
  };

  return dp(m - 1, n - 1);
}

岛屿的最大面积

题目描述

给定一个大小为 m x n 的二进制矩阵 grid。

岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直的四个方向上相邻。

可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0。

示例：

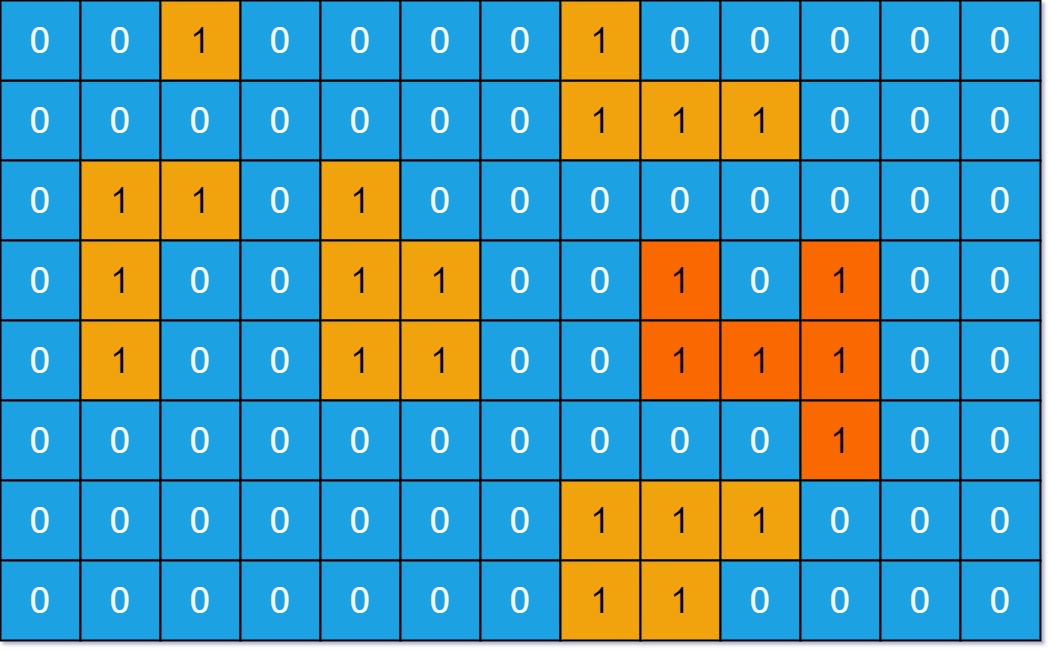
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]

输出：6

解释：答案不应该是 11，因为岛屿只能包含水平或垂直这四个方向上的 1。

思路

走到一个 grid[i][j] === 1 的地方就把它周围的 1 全部淹成 0，并且在递归时统计该区域的 1 的个数

题解

tsCopy
function maxAreaOfIsland(grid: number[][]): number {
  let max = 0;

  const dp = (i, j) => {
    if (i < 0 || j < 0 || i >= grid.length || j >= grid[0].length) {
      return 0;
    }

    if (grid[i][j] === 0) {
      return 0;
    }

    grid[i][j] = 0;

    return 1 + dp(i - 1, j) + dp(i + 1, j) + dp(i, j - 1) + dp(i, j + 1);
  };

  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[i].length; j++) {
      if (grid[i][j] === 1) {
        max = Math.max(max, dp(i, j));
      }
    }
  }

  return max;
}